고코딩
[자료구조] 트리(Tree)의 개념과 정리 본문
앞서 포스팅한 스택과 큐는 자료구조에서 선형 구조라고 한다. 선형 구조는 데이터가 순차적으로 나열되어진 형태를 말하는데, 트리는 비선형구조로 이루어져있다. 비선형구조는 데이터가 계층적(혹은 망)으로 구성되어있다. 선형구조와 비선형구조의 차이점은 구성형태뿐만 아니라 용도에서도 차이점이 들어나느데, 선형구조는 자료를 저장하고 꺼내는 것에 초점이 맞춰져 있고, 비선형구조는 표현에 초점이 맞춰져 있다. 보통 컴퓨터의 폴더 구조가 대표적인 트리의 형태를 가지고 있다.
트리(Tree)의 개념

- 계층적인 자료를 표현하는데 적합한 자료구조 이다.
- 노드(node)와 간선(edge)"브랜치(Branch)라고도 불린다" 로 구성되어 있다.
- 제일 최상위에 위치한 노드를 루트노드(Root Node)라 부르고 나머지 노드들을 서브트리(Sub Tree)라고 부른다.
- 노드와 노드는 간선으로 연결되어 있다.
전체 트리구조에서 A가 루트노드(Root Node)이고 그 밑에 존재한 나머지 {B,C,D,E,F,G,H,I,J}들은 서브 트리이다.
제일 왼쪽에 위치한 서브트리를 기준으로 보았을 때 B가 루트노드(Root Node)가 되어지고 그 밑 {E,F,G}들은 서브트리가 되어진다.
노드 간의 관계

- 노드들 간에는 부모,형제,조상,자손 관계가 존재하고 레벨이 존재한다.
- B의 입장에서 A는 부모노드(Parent Node)이며 {B,C,D}는 A의 자식노드이다.
- 같은 부모노드를 가진 자식노드들은 형제노드라고 부른다. {E,F,G}는 B의 자식노드이므로 이 3노드들은 형제 노드이다.
- H와 I는 같은 레벨에 속해 있지만 부모노드가 다르므로 형제노드가 아니다.
- 조상(ancestor) 은 노드의 부모 노드들의 총 집합이다.
- 자손(descendant) 은 노드의 서브트리에 있는 모든 노드를 지칭한다. 자식노드와 자손노드는 다른것이다.
- 레벨(level) 은 루트 노드들로부터의 깊이를 뜻한다. (루트 노드의 레벨 = 1)
- 트리의 깊이(depth of tree) 는 트리에 속한 노드의 최대 레벨을 뜻한다.
- 노드의 차수(degree) 는 어떤 노드가 가지고 있는 자식 노드의 개수이다.
- A의 경우 차수는 3 , C의 경우 차수는 1이다.
- 단말노드는 차수가 0, 즉 자식이 없는 노드이다.
- 트리의 차수 는 트리가 가지고 있는 노드의 차수 중에서 가장 큰 값이다.
N-링크 표현법
- 노드에 n 개의 링크를 두고 자식의 객수만큼 링크에 저장한다. 모든 노드는 자식 노드 수에 관계없이 최대 n개의 링크를 갖는다. 각 링크는 부속트리가 저장된 곳을 링크한다.
- 차수가 n인 경우 표현된 노드

- 거의 사용하지 않는 표현법이다.
이진트리의 정의
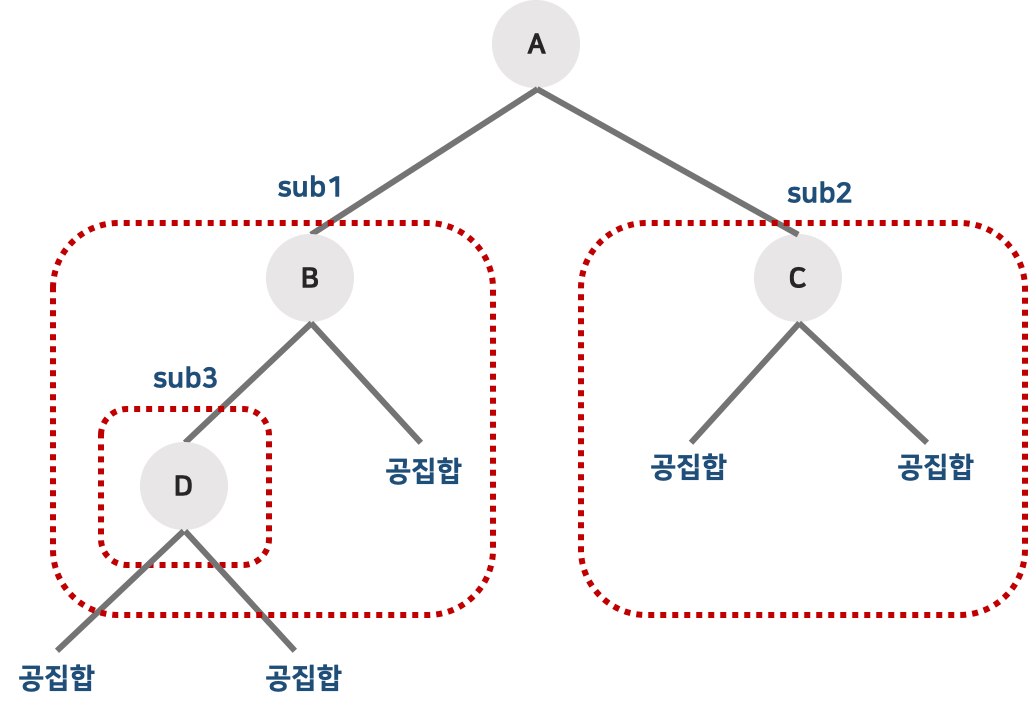
- 공집합 이거나
- 루트 와 왼쪽 서브트리, 오른쪽 서브트리 로 구성된 노드들의 유한 집합
- 공집합의 의미는 연결된 자식노드 또는 서브트리가 없다는 뜻 이다.
이진트리의 성질

- n개의 노드를 가진 이진트리는 n-1개의 간선을 가진다.
- 부모와 자신간에는 정확하게 하나의 간선만이 존재한다.

- 높이가 h인 이진트리의 경우, 최소 h개의 노드를 가지고 최대 2^h-1개의 노드를 가진다

- n개의 노드를 가지는 이진트리의 높이는 최대n이거나 최소 log(n+1)이 된다.
이진트리의 분류

- 포화 이진트리는 각 레벨에 노드가 꽉 차있는 노드를 의미한다.
- 완전 이진트리는 높이가 k일때 레벨1부터 레벨 k-1까지는 노드가 모두 채워져 있고 레벨K부터는 왼쪽부터 오른쪽으로 순서대로 노드가 채워져있다. 마지막 레벨에 노드가 꽉 차 있지 않아도 되지만 중간에 빈 곳이 있어서는 안된다.
- 포화 이진트리는 완전 이진트리에 속하지만 그 역은 성립되지 않는다.
자바로 트리 구현 - 1차원 배열/ 2차원 배열/ 노드클래스

주로 포화 이진 트리나 완전 이진 트리의 경우 많이 쓰이는 방법이다. 그 외의 이진 트리에서도 사용가능하지만 공간의 낭비가 심해진다.

보통의 인덱스는 0부터 시작하지만 계산하기 쉽게 루트 노드는 1부터 시작한다.
원하는 노드n개 까지 총 n+1 크기의 1차원 배열을 만들고 이진트리의 번호대로 노드들을 저장한다.
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int [] parent = new int[n+1];
for(int i=2 ; i<=n; i++) { //i=1이면 루트노트부터 시작하기때문에 2부터 시작
parent[i] = i/2; //노드 i의 부모노드의 인데스 = i/2
}
System.out.println(Arrays.toString(parent));
}
}자바로 트리 구현 - 2차원 배열

import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int [][] tree = new int[n][2]; //tree를 저장하기 위한 2차원 배열
for(int i=0 ; i<n ; i++) {
int a = sc.nextInt(); //노드의 번호
int b = sc.nextInt(); //노드의 왼쪽 값
int c = sc.nextInt(); //노드의 오른쪽 값
tree[a][0] = b;
tree[a][1] = c;
}
for(int i=0 ; i<n ; i++) {
System.out.println("["+tree[i][0]+","+tree[i][1]+"]");
}
}
}출력결과
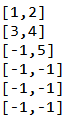
자바로 트리 구현 - 노드 클래스로 구현
현재는 전위/ 중위/ 후위 순회는 배우지 않았으니 클래스의 구조만 설명하겠다.
public class Node {
private int data; //노드의 값
private Node leftNode; //왼쪽 자식노드의 값
private Node rightNode; //오른쪽 자식노드의 값
public Node(int data, Node leftNode, Node rightNode) {
this.data = data;
this.leftNode = leftNode;
this.rightNode = rightNode;
}
public void setLeftNode(Node node) {
this.leftNode = node;
}
public void setRightNode(Node node) {
this.rightNode = node;
}
public Node getLeftNode() {
return this.leftNode;
}
public Node getRightNode() {
return this.rightNode;
}
}
public class TreeClass {
private Node newNode;
//현재는 이진트리탐색이 중요한 부분이 아니기 때문에 단순히 데이터와 좌우 자식노드만 지정해주는 기능만 넣었다.
public Node makeNode(int data, Node leftNode, Node rightNode) {
newNode = new Node(data);
newNode.setLeftNode(leftNode);
newNode.setRightNode(rightNode);
return newNode;
}
}
public class Main {
public static void main(String[] args) {
TreeClass tc = new TreeClass();
Node n50 = tc.makeNode(50, null, null);
Node n60 = tc.makeNode(60, null, null);
Node n20 = tc.makeNode(20, n50, n60);
Node n30 = tc.makeNode(30, null, null);
Node n10 = tc.makeNode(10, n20, n30);
/*
* 10
* / \
* 20 30
* / \
* 50 60
* 이런 구조의 트리 완성 root노드는 n10임
*/
}
}
간단하게 트리를 정리해 보았다. 코드를 보았으면 느끼는 것이지만 트리는 배열보다는 노드구조로 구성하는게 좀더 편하다. 트리의 특성상 노드 중간에 노드가 들어가는 경우가 있는데 배열은 데이터의 인덱스를 옮기기가 쉽지않다 트리의 특징에 알맞지 않다.
이후에는 트리의 전위,중위,후위 순회와 트리의 정렬에 대한 개념도 포스팅 하겠다.
'자료구조' 카테고리의 다른 글
| [자료구조] 힙 개념과 JAVA로 구현 (1) | 2021.01.06 |
|---|---|
| [자료구조] 이진트리의 순회 및 java구현 (0) | 2020.12.29 |
| [자료구조] JAVA로 큐(Queue)구현 (1) | 2020.12.28 |
| [자료구조]JAVA로 스택(Stack)구현 (1) | 2020.12.28 |
| [자료구조] 자료구조의 정리 (0) | 2020.12.28 |




